- Nilai & Vektor Eigen
Ax = lx
Contoh :
Vektor x = [1,2] adalah vektor eigen dari :
Untuk menghitung
nilai eigen matrik A
yang berorodo
nxn tulislah
Ax
= lx
sebagai,
Ax
= l.I.x
(lI – A)x = 0
Persamaan
terakhir
adalah polinomial l berderajad n yang disebut dengan persamaan karakteritik A, sedangkan nilai eigen matrik A adalah akar-akar persamaan karakteristik A (akar-akar polinomial dalam l).
Langkah-langkah menentukan nilai eigen dan vektor eigen matrik A adalah :
(1)Bentuk matrik (lI – A)
(2)Hitung determinan,
det(lI – A)=0
(3)Tentukan
persamaan
karakteristik dari, (lI – A) = 0
(4)Hitung akar-akar
persamaan
karakteristik (nilai lamda)
(5)Hitung vektor eigen dari SPL,
(lI
– A)x=0
Contoh:
Carilah nilai eigen dan vektor eigen dari
Jawab:
Bentuk, lI – A yaitu :
Persamaan
karakteristiknya adalah :
Akar-akar
persamaan
karakteristiknya adalah :
Vektor
eigen x
dari A diperoleh
dari :
(lI
– A)x
= 0
Untuk l = 1, diperoleh SPL
Untuk l = 2 dan l = 3, kalian dapat mencoba caranya sendiri seperti diatas, hasilnya adalah
Jadi vektor eigen yang
bersesuaian
dengan :
l= 1 adalah x = [1,1,1] ;
l= 2 adalah x = [2,3,3] ;
l= 3 adalah x = [1,3,4]
- Diagonalisasi
Matrik bujur sangkar
A dikatakan
dapat didiagonalisasi jika terdapat matrik P yang mempunyai invers sedemikian rupa sehingga, P–1AP
adalah matrik
diagonal. Matrik P dikatakan
mendiagonalisasi A.
Langkah-langkah menentukan matrik P dan D adalah sebagai berikut :
(1). Hitung persamaan karakteristik A nilai eigen
(2). Carilah n vektor eigen bebas linier A sesuai nilai eigen, p1,p2, ... , pn,
(3). Bantuklah matrik P = [p1 p2 … pn]
dan hitunglah
P–1
(4). Hitung, D = P–1AP dengan diagonal utama, l1, l2, … ,ln
Contoh:
Tentukan diagonalisasi dari matrik

Jawab:
Dari hasil vektor eigen yang sudah dicari diatas, dapat kita rangkai menjadi matrik, sehingga menjadi
Untuk mencari diagonalisasi terdapat rumus, yaitu:
P-1 adalah invers matrik dari P dan diperoleh
Sehingga diagonalisasi dapat kita cari







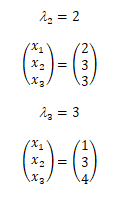







Tidak ada komentar:
Posting Komentar