Apa itu Invers Matriks?
Invers Matriks dilambangkan dengan pangkat minus satu ( …-1 ), misalnya diketahui sebuah matrik A maka invers dari matrik A adalah A-1 .
Suatu matriks dikatakan memiliki invers, jika matriks tersebut dikalikan dengan invers matriknya akan menghasilkan sebuah matrik identitas, misal terdapat suatu matrik yang diberi nama matrik A, maka invers matrik A dikali dengan matrik A akan sama dengan matrik A dikali invers matrik A dan mengahasilkan matrik indentitas.
A.A–1 = A–1.A = I
Metode Penyelesaian Invers Matriks
Ada beberapa cara atau metode untuk menyelesaikan invers matrik,yaitu:
- Metode Adjoint Matrik
- Metode Operasi Baris Elementer
- Metode Perkalian Invers Matrik Elementer
- Metode Partisi Matrik
Berikut adalah penjelasan dari keempat metode tersebut:
- Metode Adjoint Matrik
Adjoint Matrik dinotasikan dengan Adj(...), misal diketahui matrik A, maka adjoint dari matrik A bisa dinotasikan dengan Adj(A). Adjoint matrik A adalah transpose dari matriks yang elemen-elemennya merupakan kofaktor-kofaktor dari elemen matriks A.
Adj(A)=(kof(A))T
Rumus dari adjoint A adalah:
Sedangkan rumus invers matriks menggunakan metode adjoint adalah:
Contoh soal:
Kasus Matriks berordo 3x3
Diketahui sebuah matrik A berordo 3x3, tentukan invers matriks A
Jawab:
det(A) bisa kita cari dengan berbagai, saya telah membahas pada postingan sebelum ini tentang Pengertian, Sifat-sifat, dan Penyelesaian Determinan Matriks, sedangkan minor matriks saya bahas dalam Transpose, Minor, dan Kofaktor Matriks.
Maka langkah selanjutnya adalah
Setelah kita memperoleh minor-minor dari unsur matrik tersebut, maka selanjutnya kita mentransposenya.
Maka invers dari matrik A adalah
Kasus Matriks berordo 4x4
Diketahui sebuah matrik B berordo 4x4, tentukan invers dari matrik B
Jawab:
Untuk soal matriks berordo 4x4 ini, saya telah membahas mencari determinannya menggunakan metode doolittle dan crout dipostingan sebelumnya Pengertian, Sifat-sifat, dan Penyelesaian Determinan Matriks, sehingga untuk determinannya saya langsung tulis saja hasilnya.
Selanjutnya kita transpose, sehingga menjadi
Maka invers dari matrik B adalah
- Metode Operasi Baris Elementer
Setelah kita mengetahui penyelesaian menggunakan metode adjoint, maka sekarang kita akan belajar cara yang lainnya yaitu Operasi Baris Elementer (OBE).
Contoh Soal:
Tentukan invers matrik dari matrik berikut menggunakan metode operasi baris elementer (obe)!
Tentukan invers matrik dari matrik berikut menggunakan metode operasi baris elementer (obe)!
Jawaban:
Karena baris 1 kolom 1 sudah bernilai 1, maka langsung
selesaikan yang baris 2
Baris 4 kolom 2 sudah
bernilai 0, maka langsung ke baris 1
Baris 3 kolom 4 sudah 0, maka langsung ke baris 2
- Metode Perkalian Baris Elementer
Untuk perkalian baris elementer ini, saya akan menggunakan contoh soal yang sama dengan contoh soal Operasi Baris Elementer, yang membedakan hanya metode pengerjaannya saja dan hasilnya nanti harus sama dengan hasil invers yang sebelumnya.
Contoh:
Tentukan invers matrik dari sebuah matrik dibawah ini menggunakan metode perkalian baris elementer!
Jawab:
Menghitung E1
Menghitung
E2
Menghitung E3
Menghitung E4
- Metode Partisi Matrik
Pada prinsipnya metode partisi matrik adalah membagi suatu matrik menjadi 4 bagian, untuk contohnya saya masih menggunakan matrik yang sama dengan sebelumnya namun cara atau mentodenya yang berbeda.
Contoh:
Tentukan invers matrik dari suatu matrik berikut menggunakan metode partisi matrik!
Jawab:
Gimana materinya??
Demikian materi tentang invers matrik mudah-mudahan bermanfaat bagi saya dan juga para pembaca blog ini aminn...








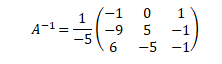


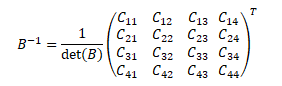
























Tidak ada komentar:
Posting Komentar